Two Lefts Don't Make a Right, But...

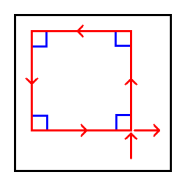Imagine you are driving a car that can only turn left. (I guess it would make sense for this car to be blue.) You come to an intersection and need to turn right. What can you do? Assuming the streets are laid out in basic city blocks, you can go straight and then make three consecutive lefts, circling the block (squaring the block?...). Upon returning to the original intersection, you can continue on in the desired direction. Apparently three lefts make a right.

Right?

Well, not always. This is only true for flat space (or in better math terms, 2-D Euclidean space). If the space we are talking about is curved then things change. Consider embarking on a journey that begins at the North Pole. You head due south and then make a 90-degree turn east when you hit the equator. After traveling 1/4 around the earth, you make a 90-degree turn back north. Following this path will lead you right back to the North Pole. So we find that two right angle turns will bring us back to where we started. In the city block situation, it took three right angle turns. See the difference? This is the basics of curved space (or space-time).

This means that two lefts can make a right.

For much better pictures than my MS Paint work, see Wikipedia's Non-Euclidean geometry.